In a right angle ΔABC is which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at PQ bisects BC.
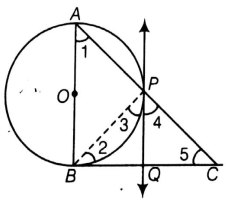
Given : In a right angle ΔABC is which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Also PQ is a tangent at P
To Prove : PQ bisects BC i.e. BQ = QC
Proof :
∠APB = 90° [Angle in a semicircle is a right-angle]
∠BPC = 90° [Linear Pair ]
∠3 + ∠4 = 90 [1]
Now, ∠ABC = 90°
So in △ABC
∠ABC + ∠BAC + ∠ACB = 180°
90 + ∠1 + ∠5 = 180
∠1 + ∠5 = 90 [2]
Now ,
∠ 1 = ∠ 3[angle between tangent and the chord equals angle made by the chord in alternate segment]
Using this in [2] we have
∠3 + ∠5 = 90 [3]
From [1] and [3] we have
∠3 + ∠4 = ∠3 + ∠5
∠4 = ∠5
QC = PQ [Sides opposite to equal angles are equal]
But Also PQ = BQ [Tangents drawn from an external point to a circle are equal]
So, BQ = QC
i.e. PQ bisects BC .