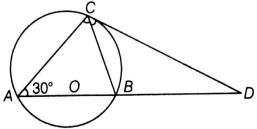
Given : AB is a diameter of a circle, AB is a diameter and AC is a chord Also ∠BAC = 30° .The tangent at C intersects extended AB at a point D

To Prove : BC = BD

Proof :

∠CAB = ∠BCD =30° [1] [angle between tangent and chord is equal to angle made by chord in alternate segment]

Now, ∠ACB = 90° [Angle in a semicircle is a right angle]

∠ACD = ∠ACB + ∠BCD = 90 + 30 = 120°

In triangle ACD, By Angle Sum Property

∠ACD + ∠CAD + ∠ADC = 180°

120 + ∠CAB + ∠BDC = 180°

120 + 30 + ∠BDC = 180

∠BDC = 30° [2]

From [1] and [2]
∠BCD = ∠BDC = 30°

BD = BC [Angles opposite to equal sides are equal]

Hence Proved !