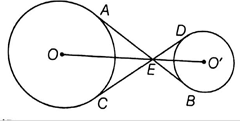
Given : AB and CD are two tangents with centers O and O' intersect at E .

To Prove : O, E and O' are collinear.

Construction : Join AO, OC O'D and O'B

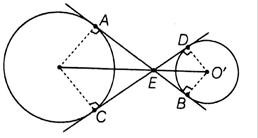
In △AOE and △EOC

OA = OC [radii of same circle]

OE = OE [common]

AE = EC [Tangents drawn from an external point to a circle are equal]

△AOE ≅ △EOC [By Side Side Side Criterion]

∠AEO = ∠CEO [Corresponding parts of congruent triangles are equal ]

∠AEC = ∠AEO + ∠CEO = ∠AEO + ∠AEO = 2∠AEO [1]

Now As CD is a straight line

∠AED + ∠AEC = 180° [linear pair]

2∠AEO = 180 - ∠AED [From 1]

[2]

Now, In △O'ED and △O'EB

O'B = O'D [radii of same circle]

O'E = O'E [common]

EB = ED [Tangents drawn from an external point to a circle are equal]

△O'ED ≅ △O'EB [By Side Side Side Criterion]

∠O'EB = ∠O'ED [Corresponding parts of congruent triangles are equal ]

∠DEB = ∠O'EB + ∠O'ED = ∠O'ED + ∠O'ED = 2∠O'ED [3]

Now as AB is a straight line

∠AED + ∠DEB = 180 [Linear Pair]

2∠O'ED = 180 - ∠AED [From 3]

[4]

Now,

So O, E and O' lies on same line [By the converse of linear pair]

Hence Proved.