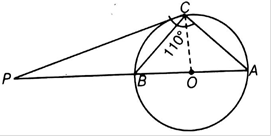
Given : A circle with center O in which PC is a tangent a point C and AB is a diameter which is extended to P and ∠PCA = 110°

To Find : ∠CBA

∠ACB = 90° [Angle in a semicircle is a right angle] [1]

Also,

∠PCA = ∠ACB + ∠PCB

110 = 90 + ∠PCB

∠PCB = 20°

Now, ∠PCB = ∠BAC [angle between tangent and the chord equals angle made by the chord in alternate segment]

∠BAC = 20° [2]

Now In △ABC By angle sum property of Triangle.

∠CBA + ∠BAC + ∠ACB = 180

∠CBA + 20 + 90 = 180

∠CBA = 70°