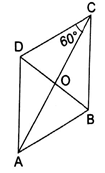
Given:∠DCB = 60°

Let the length of the side be x

Here, consider ΔBCD

BC = DC (all sides of rhombus are equal)

∴ ∠CDB = ∠CBD (angles opposite to equal sides are equal)

Now, by angle sum property

∠CDB + ∠CBD + ∠BCD = 180°

2× ∠CBD = 180° –60°

2 × ∠CBD = 180° – 60°

∴ 2× ∠CBD = 120°

∠ CBD = = 60°

∴ ∠CDB = ∠CBD = 60°

∴ Δ ADC is equilateral triangle

∴ BC = CD = BD = x cm

In Rhombus diagonals bisect each other.

Consider Δ COD

By Pythagoras theorem

CD² = OD² + OC²

x² = ² + OC²

OC² = x² – ²

OC =

OC = cm

∴ AC = 2× OC = 2 × = x

AC: BD = x : x = : 1

∴ AC: BD = : 1