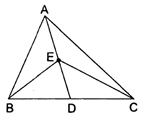
Given:

Here,

D is the midpoint of BC and AD is the median of ΔABC

Area (Δ ABD) = Area (Δ ADC) (∵ median divides the triangle into two triangles of equal areas)

∴ Area (Δ ABD) = Area (Δ ADC) = 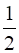Area (∆ABC)

Now, consider Δ ABD

Here, BE is the median

Area (Δ ABE) = Area (Δ BED)

∴ Area (Δ ABE) = Area (Δ BED) = 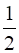Area (∆ABD)

Area (Δ BED) = 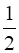Area (∆ABD)

Area (Δ BED) = 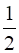× 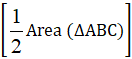(∵Area (Δ ABD) = 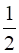Area (∆ABC) ) –1

Area (Δ BED) = 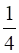Area (∆ABC)

Similarly,

Area (Δ EDC) = 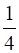Area (∆ABC) –2

Add –1 and –2

Area (Δ BED) + Area (Δ EDC) = 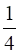Area (∆ABC) + 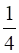Area (∆ABC) = 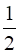Area (∆ABC)

∴ Area (Δ BEC) = 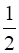Area (∆ABC)