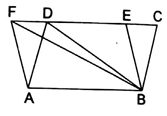
Given: area of ‖ gm ABCD is 80 cm²

We know that any two or parallelogram having the same base and lying between the same parallel lines are equal in area.

∴ ar(||gm ABCD) = ar(||gm ABEF) –1

We also know that when a parallelogram and a triangle lie on same base and between same parallel lines then, area of the triangle is half the area of the parallelogram.

∴ ar(∆ABD) = 1/2 × ar(||gm ABCD) and,

ar(∆BEF) = 1/2 × ar(||gm ABEF)

(i)

ar(||gm ABCD) = ar(||gm ABEF)

∴ ar(||gm ABEF) = 80cm² (∵ar(||gm ABCD) = 80cm²)

(ii)

ar(∆ABD) = 1/2 × ar(||gm ABCD)

ar(∆ABD) = 1/2 × 80 = 40cm² (∵ar(||gm ABCD) = 80cm²)

∴ ar(∆ABD) = 40cm²

(iii)

ar(∆BEF) = 1/2 × ar(||gm ABEF)

ar(∆BEF) = 1/2 × 80 = 40cm² (∵ar(||gm ABEF) = 80cm²)

∴ ar(∆BEF) = 40cm²