∆ ABC and ∆BDE are two equilateral triangles such that D(E) is the midpoint of BC. Then, prove that ar(∆BDE) = ar(∆ABC).

Question

Philoid · Accepted Answer

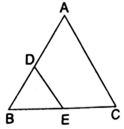
Given:∆ABC and ∆BDE are two equilateral triangles, D is the midpoint of BC.

Consider ΔABC

Here, let AB = BC = AC = x cm (equilateral triangle)

Now, consider ΔBED

Here,

BD = 1/2 BC

∴ BD = ED = EB = 1/2 BC = x/2 (equilateral triangle)

Area of the equilateral triangle is given by: (a is side length)

∴ ar(∆BDE): ar(∆ABC) = := :1 = 1:4

That is =

∴ ar(∆BDE) = ar(∆ABC)

Hence Proved