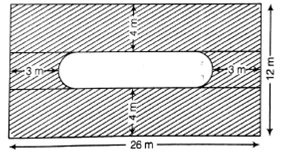
Find the area of the shaded region in figure.
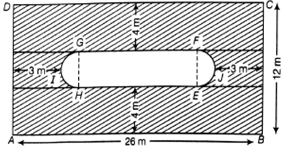
Label the figure as above.
Area of the shaded region = Area of the rectangle ABCD – (Area of the rect. EFGH + (Area of the semi-circle EFJ +Area of the semi-circle GHI)
Length and breadth of outer rect. ABCD are 26 m and 12 m respectively.
∴ Area of the rect. ABCD = Length × Breadth = AB × BC = 26 × 12 = 312 m2
From the figure, length and breadth of inner rect. EFGH are (26-5-5) m and (12-4-4) m, i.e. 16 m and 4 m respectively.
∴ Area of the rect. EFGH = Length × Breadth
= EF × FG
= 16 × 4 = 64 m2
Breadth of the inner rectangle = Diameter of the semi-circle EJF = d = 4m
∴ Radius of semi-circle EJF = r = 2 m
Area of the semi-circle EFJ = Area of the semi-circle GHI = πr2/2 = 4π/2 = 2π m2
∴ Area of shaded region = 312 – (64 + 2π + 2π)m2 = ( 248 – 4π ) m2