The central angles of two sectors of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
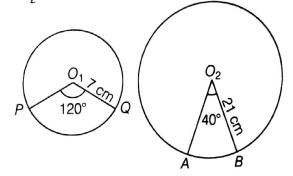
Radius of one sector = r1 = 7 cm
Radius of second sector = r2 = 21 cm
Central angle of one sector = 120°
Central angle of second sector = 40°
Central angle of one sector (in radians) = θ1 = (120π/180)
Central angle of second sector (in radians) = θ2 = (40π/180)
Area of first sector = ![]()
![]()
= ![]() =
=
154/3 = 51.33 cm2
Area of second sector = ![]()
= ![]()
![]()
= 154 cm2
Let the lengths of the corresponding arc be l1 and l2.
Now, arc length of first sector = Radius × Central Angle (in radians)
= ![]() = 44/3 cm
= 44/3 cm
Now, arc length of second sector = Radius × Central Angle (in radians)
= ![]() = 44/3 cm
= 44/3 cm
Hence, we observe that arc lengths of two sectors of two different circles may be equal but their area need not be equal.