In ∆PQR and ∆MST, ∠ P = 55°, ∠ Q = 25°, ∠ M = 100° and ∠ S = 25°. Is ∆QPR ∼ ∆TSM? Why? (True)

Question

Philoid · Accepted Answer

We know that,

The sum of three angles of a triangle is 180°.

In ∆PQR,

∠P + ∠Q + ∠R = 180°

⇒ 55° + 25° + ∠R = 180°

⇒ ∠R = 180° - (55° + 25°) = 180°- 80° = 100°

Similarly, in ∆TSM,

∠T + ∠S + ∠M = 180°

⇒ ∠T + ∠25° + 100° = 180°

⇒ ∠T = 180°- (∠25° + 100°)

⇒ ∠T = 180° - 125° = 55°

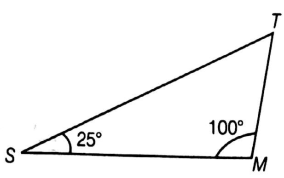
In ∆PQR and ∆TSM,

∠P = ∠T,

∠Q = ∠S

And

∠R = ∠M

So, ∆PQR ∼ ∆TSM

Since, all corresponding angles are equal

Hence,

∆QPR is similar to ∆TSM,