In a ∆PQR, PR 2 = QR 2 and M is a point on side PR such that QM ⊥ PR. Prove that QM 2 = PMXMR.

Question

Philoid · Accepted Answer

Given,

∆PQR,

PR² = QR² and QM⊥PR

Since,

By Pythagoras theorem,

PR² – PQ² = QR²

⇒ PR² = PQ² + QR²

So, ∆PQR is right angled triangle at Q.

In ∆QMR and ∆PMQ,

∠M = ∠M [each]

∠MQR = ∠QPM [each equal to 90°-∠R]

So, by AAA similarity criteria,

∴ ∆QMR ∼ ∆PMQ

Now, using property of area of similar triangles, we get,

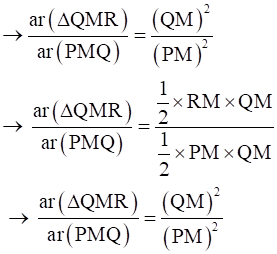
[∵ Area of triangles = × base × height]

⇒ QM² = PM × RM

Hence proved.