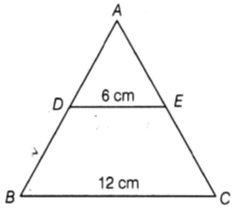
Given,

DE || BC,

DE = 6 cm and BC = 12 cm

In ∆ABC and ∆ADE,

∠ABC = ∠ADE [corresponding angle]

∠ACB = ∠AED [corresponding angle]

And

∠A = ∠A [common side]

∴ ∆ABC ∼ ∆AED [by AAA similarity criterion]

Then,

By property of area of similar triangle,

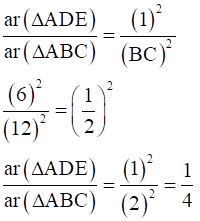
Let area (∆ADE) = k,

Then area (∆ABC) = 4k

Now,

Area (DECB) = area (ABC) – area (ADE) = 4k – k = 3k

∴ Required ratio = area (ADE) : area (DECB) = k : 3k = 1:3