In given figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3cm, then find BD.
Given,
AC = 8 cm,
AD = 3 cm and ∠ACB = ∠CDA
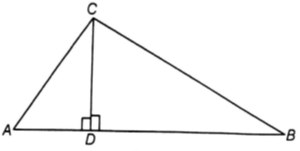
From figure,
∠CDA = 90°
∴ ∠ACB = ∠CDA = 90°
In right angled ∆ADC,
AC2 = AD2 + CD2
⇒ (8)2 = (3)2 + (CD)2
CD2 = 64 – 9 = 55
⇒ CD = √55 cm
In ∆CDB and ADC.
∠BDC = ∠AD [each 90°]
∠DBC = ∠DCA [each equal to 90°-∠A]
∴ ∠CDB ∼ ∆ADC
Then,

⇒ CD2 = AD × BD
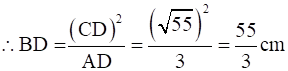
14