A 15 high tower casts a shadow 24 long at a certain time and at the same time, a telephone pole casts a shadow 16 long. Find the height of the telephone pole.
Given,
Let,
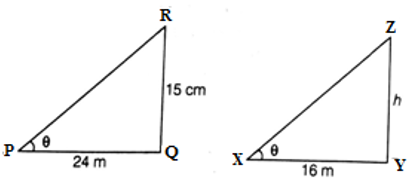
QR = 15 m (height of tower)
PQ = 24 m (shadow of tower)
At that time ∠RPQ = θ
Again, let YZ = h be a telephone pole and its shadow XY = 16 m.
The same time ∠YXZ = θ
Here, ABC and ∆DEF both are right angles triangles.
In ∆PQR and ∆XYZ,
∠RPQ = ∠YXZ = θ
∠Q = ∠Y [each 90°]
∴ ∆PQR ∼ ∆XYZ [by AAA similarity criterion]
Then,
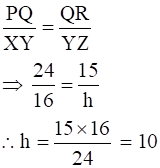
Hence, the height of the telephone pole is 10 m.
15