Let a ∆ABC in which a line DE parallel to BC intersects AB at D and AC at E.

To prove DE divides the two sides in the same ratio.

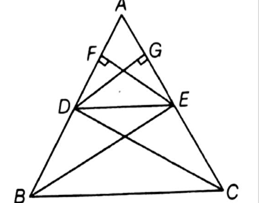
Construction join BE, CD and draw EF ⊥ AB and DG ⊥ AC.

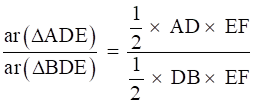
Proof Here,

[ area of triangle = × base × height]

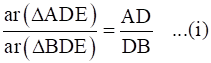
Similarly,

Now,

Since,

∆BDE and ∆DEC lie between the same parallel DE and BC and on the same base DE.

So, area (∆BDE) = area(∆DEC) …..(iii)

From Equation (i), (ii) and (iii),

AD/DB = AE/EC

Hence proved.