Given,

PQRS is a parallelogram,

So, PQ || SR and PS || QR.

Also, AB || PS.

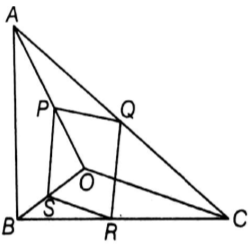
To prove OC || SR

In ∆OPS and OAB,

PS | | AB

∠POS = ∠AOB [common angle]

∠OSP = ∠OBA [corresponding angles]

∴ ∆OPS ∼ ∆OAB [by AAA similarity criteria]

Then,

PS/AB = OS/OB …(i) [by basic proportionality theorem]

In ∆CQR and ∆CAB,

QR || PS || AB

∠QCR = ∠ACB [common angle]

∠CRQ = ∠CBA [corresponding angles]

∴ ∆CQR ∼ ∆CAB

Then, by basic proportionality theorem

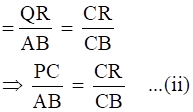
[PS ≅ QR Since, PQRS is a parallelogram,]

From Equation (i) and (ii),

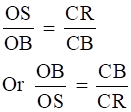
On subtracting from both sides, we get,

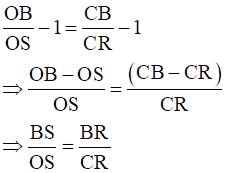
By converse of basic proportionality theorem, SR || OC

Hence proved.