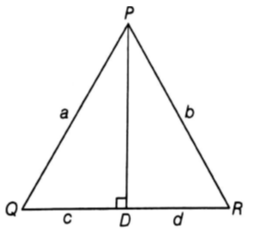
In ∆PQR, PD ⊥ QR such that D lies on QR, if PQ = a, PR = b, QD = c and DR = d, then prove that (a + b)(a - b) = (c + d)(c - d).
Given,
In ∆PQR,
PD⊥QR,
PQ = a, PR = b, QD = c and DR = d
in right angled ∆PDQ,
PQ2 = PD2 + QD2 [by Pythagoras theorem]
= a2 = PD2 + c2
= PD2 = a2 – c2 …..(i)
In right angled ∆PDR,
PR2 = PD2 + DR2 [by Pythagoras theorem]
= b2 = PD2 + d2
= PD2 = b2 - d2 ……(i)
From Equation (i) and (ii),
A2 - c2 = b2 - d2
A2 - b2 = c2 - d2
= (a – b) (a + b) = (c – d) (c + d)
Hence proved.
11