Given,

⎩||m and line segment AB, CD and EF are concurrent at point P.

To prove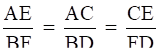

in ∆APC and ∆BPD,

∠APC = ∠BPD [vertically opposite angles]

∠PAC = ∠PBD [alternate angles]

∴ ∆APS-BPD [by AAA similarity criterion]

Then,

In ∆APE and ∆BPF,

∠APE = ∠BPF [vertically opposite angles]

∠PAE = ∠PBF [alternate angles]

∴ ∆APE ∼ ∆BPF [by AAA similarity criterion]

Then,

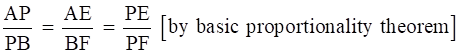
In ∆PEC and ∆PED,

∠EPC = ∠FPD [Vertically opposite angles]

∠PCE = ∠PDF [alternate angles]

∴ ∆PEC ∼ ∆PFD [by AAA similarity criterion]

Then,

From Eqs. (i), (ii) and (iii),

Hence proved.