Given,

in ∆ABC, E is the mid-point of CA and ÐAEF = ÐAFE

To prove BD/CD = BF/CE

Construction take a point G on AB such that CG‖EF.

since, E is the mid-point of CA.

∴ CE = AE……(i)

In ∆ACG,

CG‖EF and E is mid-point of CA.

So, CE = GF…(ii) [by mid-point theorem]

Now, in ∆BCG and ∆BDF,

CG || EF

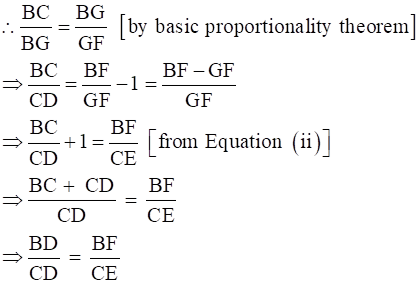
Hence proved.