Prove that the area of the semi-circle drawn on the hypotenuse of a right-angled triangle is equal to the sum of the areas of the semi-circles drawn on the other two sides of the triangle.
Let RST be a right triangle at S and RS = y, ST = x.
Three semi-circles are draw on the sides RS, ST and RT, respectively A1, A2 and A3.
To prove A3 = A1 + A2
In ∆RST,
by Pythagoras theorem,
RT2 = RS2 + ST2
= RT2 = y2 + x2
![]()
We know that,
Area of a semi-circle with radius, 
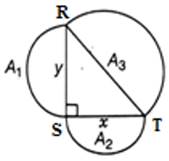
∴ Area of semi-circle drawn on RT,
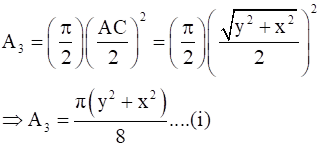
Now, area of semi-circle drawn on RS, 
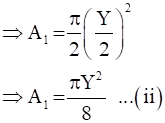
And area of semi-circle drawn on ST,
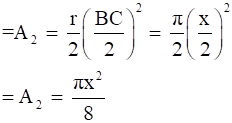
On adding Equation (ii) and (iii), we get
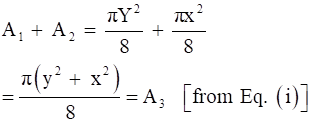
⇒ A1 + A2 = A3
Hence proved.
17