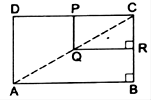
In the adjoining figure, ABCD and PQRC are rectangles, where Q is the mid-point of AC.

Question

In the adjoining figure, ABCD and PQRC are rectangles, where Q is the mid-point of AC. Prove that (i) DP = PC (ii)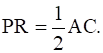

Philoid · Accepted Answer

(i) Here, we have

∠CRQ = ∠CBA = 90^o

Thus, RQ ∣∣ AB

Now, In ∆ABC,

Q is the mid-point of AC and QR ∣∣ AB.

Thus, R is the mid-point of BC.

In the same way, P is the midpoint of DC.

Hence, DP = PC

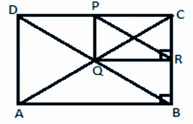
(ii) Here, let us join B to D.

Now, In ∆CDB,

P and R are the mid points of DC and BC respectively.

Since, AC = BD

Thus, PR ∣∣ DB and PR = DB = AC