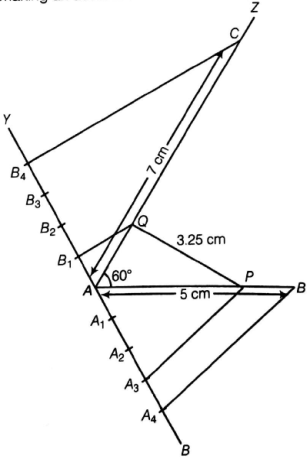
Two-line segment AB and AC include an angle of 60°, where AB=5cm and AC=7cm. Locate points P and Q on AB and AC, respectively such that AP= 3/4 AB and AQ= 1/4 AC. Join P and Q and measure the length PQ.
Given,
AB=5cm
AC=7cm
AP = 3/4 AB and AQ = 1/2 AC … (i)
From equation-(i)
AP = 3/4 × AB = 3/4 × 5 = 15/4 cm
![]() P is any point on the AB
P is any point on the AB
![]() PB=AB-AP
PB=AB-AP
PB = 5 – 15/4
= 5/4 cm
∴ AP: PB = 15/4 : 5/4
⇒ AP: PB = 3: 1
i.e. the scale factor of line segment AB is 3/1.
From Eq. (i).
AQ=1/4 AC
= 1/4 × 7 = 7/4 cm
![]() Q is any point on the AC
Q is any point on the AC
![]() QC = AC – AQ
QC = AC – AQ
QC = 7 – 7/4
= 21/4 cm
∴ AQ : QC = 7/4 : 21/4 = 1:3
⇒ AQ : QC = 1: 3
i.e. scale factor of line segment AQ is 1/3.
Steps of construction
1. Draw a line AB=5cm.
2. Draw a ray AZ making an acute angle, ∠ BAZ=60°.
3. With A as center and radius equal to 7 cm draw an arc cutting the line AZ at C.
4. Draw a ray AX, (make acute ∠BAX).
5. Along AX, mark 4 points A1, A2, A3, and A4
Such that A1A2=A1A3=A3A4
6. Join A4B
7. Draw A3P||A4B meeting AB at P.
[by making an angle equal to ∠AA4 B]
Then, P is the point on AB which divides it in the ratio 3:1.
So, AP: PB=3:1
8. Draw a ray AY, making an acute ∠CAY.
9. Along AY, mark 4 point B1B2, B3and B4.
Such that AB1=B1B2=B2B3=B3B4
10. Join B4C.
11. Draw B1Q||B4C meeting AC at Q.
[by making an angle equal to∠AB4C]
Then, Q is the point on AC which divides it in the ratio1:3.
So, AQ:QC=1:3
12. Finally, join PQ and its measurement is 3.25cm.