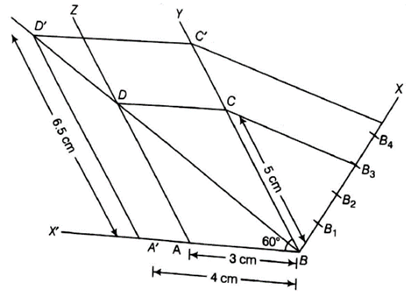
Draw a parallelogram ABCD in which BC=5 cm, AB=3 cm, and ∠ ABC=60 ° , divide it into triangles BCD and ABD by the diagonal BD. Construct the triangles BD ’ C ’ similar to ∆BDC with scale factor 4/3 . Draw the line segment D’A’ parallel to DA, where A’ lies on extended side BA. Is A’BC’D’ a parallelogram?

Question

Philoid · Accepted Answer

Steps of construction

1. Draw a line AB=3 cm.

2. Draw a ray BY making an acute ∠ABY=60°.

3. With B as center and radius equal to 5 cm draw an arc cut the point C on BY.

4. Draw a ray AZ making an acute ∠ZAX’=60°.(BY││AZ, ∴ ∠YBX’=ZAX’=60°)

5. With A as center and radius equal to 5 cm draw an arc cut the point D on AZ.

6. Join CD and finally make a parallelogram ABCD.

7. Join BD, which is a diagonal of parallelogram ABCD.

8. Draw any ray BX downwards making an acute ∠CBX.

9. Locate 4 points B₁,B₂,B₃,B₄ on BX, such that BB₁=B₁B₂=B₂B₃=B₃B₄.

10. Join B₄C and from B₃C draw a line B₄C’||B₃C intersecting the extended line segment BC at C’.

11. Draw C’D’CD intersecting the extended line segment BD at D’. Then, ∆D’BC’ is the required triangle whose sides are 4/3 of the corresponding sides of ∆DBC.

12. Now draw a line segment D’A’DA, where A’ lies on the extended side BA

13. Finally, we observe that A’BC’D’ is a parallelogram in which A’D’=6.5 cm A’B = 4 cm and ∠A’BD’= 60° divide it into triangles BC’D’ and A’BD’ by the diagonal BD’.