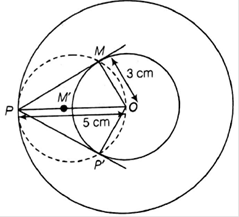
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.

Given, two concentric circles of radii 3 cm and 5 cm with center O. We have to draw a pair of tangents from point P on outer circle to the other.

Steps of construction


1. Draw two concentric circles with center O and radius 3 cm and 5 cm.


2. Take any point P on the outer circle. Join OP.


3. Bisect OP, let M’ be the mid-point of OP.


Taking M’ as a centre and OM’ as radius draw a circle dotted which cute the inner circle at M and P’.


4. Join PM and PP’. Thus, PM and PP’ are required tangents.


5. On measuring PM and PP’, we find that PM=PP’=4 cm.


In ∆OMP,


∠PMQ=90°


∴ PM2=OP2=4cm


PM2=(5)2-(3)2=25-9=16


PM = 4 cm


Hence, the length of both tangents is 4 cm.



3