Draw a circle of circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60°. Also justify the construction, Measure the distance between the centre of the circle and the point of intersection of tangents.
Steps of construction
1. Draw a circle of radius OA=4 cm.
2. Produce OA to B such that OA=AB=4 cm,
3. A as the centre draw a circle of radius AO=AB=4 cm. Suppose it cuts the circle drawn in step 1 at P and Q.
4. Join BP and BQ to get desired tangents.
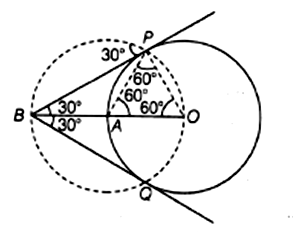
In ∆OAP,
OA=OP=4 cm
[![]() Radius]
Radius]
Also,
AP=4 cm
[![]() Radius of circle with center A]
Radius of circle with center A]
∴ ∆OAP is equilateral
⇒ ∠PAO=60°
⇒ ∠BAP=120°
In ∆BAP,
BA=AP and ∠BAP=120°
∴ ∠ABP= ∠APB=30°
⇒ ∠PBQ=60°
6