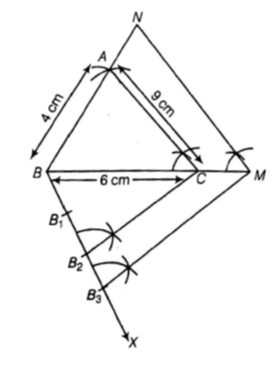
Draw a ∆ABC in which AB=4 cm, BC=6 cm, and AC= 9 cm. Construct a triangle similar to ∆ABC with scale factor 3/2. Justify the construction. Are the two triangles congruent? Note that, all the three angles and two sides of the two triangles are equal.
Steps of construction
1. Draw a line BC=6 cm.
2. B and C as centers, draw two arcs of radii 4 cm and 9 cm intersecting each other at A.
3. Join BA and CA, ∆ABC is the required triangle.
4. Draw any ray BX downwards making an acute angle.
5. Mark 3 points B1,B2,B3 on BX, such that BB1=B1B2=B2B3.
6. Join B2C and draw B3M││B2C intersecting the extended line segment BC at M.
7. Draw MN││CA intersecting the extended line segment BA to N.
Then,
∆NBM is the required triangle whose sides are equal to 3/2 of the corresponding sides of the ∆ABC.
B3M││B2C
∴ ![]()

= 1 + CM/BC
= 1 + 1/2
= 3/2
MN![]() CA
CA
∴ ∆ABC ̴ ∆NBM
∴ 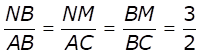
The two triangles are not congruent because, if two triangles are congruent, then they have the same shape and the same size.
Here, all the three angles are same but three sides are not same i.e., one side is different.