Let the length breath and height be the external dimension of an open box and thickness be

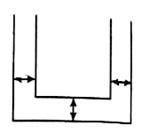
The volume of metal used in box = Volume of external box - Volume of internal box

For external box,

Length, l = 36 cm

Breadth, b = 25 cm

Height, h = 16.5 cm

We know that,

Volume of cuboid = lbh

Where, l, b and h are the length, breadth and height of tank respectively

Volume of external box = 36(25)(16.5) = 14850 cm³

Now,

As the box is open from top,

For internal box,

Length, l' = Length of external box - 2(thickness of box) = 36 - 2(1.5) = 33 cm

[i.e. the thickness of two sides is deduced]

Breadth, b' = Breadth of external box - 2(thickness of box) = 25 - 2(1.5) = 22 cm

[i.e. the thickness of two sides is deduced]

Height, h' = Height of external box - thickness of box = 16.5 - 1.5 = 15 cm

[i.e. the thickness of bottom is reduced]

Volume of internal box = 33(22)(15) = 10890

So,

Volume of metal in box = 14850 - 10890 = 3960 cm³

Also,

1 cm³ weighs 7.5 g

3960 cm³ weighs 3960(7.5) = 29,700 g

So,

The weight of box is 29,700 g i.e. 29.7 kg