A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains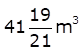 
of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
Let the radius of surmounted hemispherical dome = r
Diameter of hemispherical dome = 2r
Given,
Total height of dome = 2r
Height of hemispherical part = Radius of hemispherical part = r
Height of cylindrical part = r
As we know,
Volume of cylinder = πr2h
Where r is base radius and h is height of cylinder.
Volume of cylindrical part = πr2r = πr3 cm3
Also,
, where r is radius of hemisphere.
Volume of conical part
Volume of building = Volume of cylindrical part + volume of conical part
Volume of building 
Volume of air in building = volume of building
r3 = 8
r = 2 m
Height of building = 2r = 2(2) = 4 meter