If 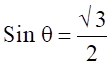 , find all the values of all the trigonometric ratios of θ.
, find all the values of all the trigonometric ratios of θ.
We have, ![]() = perpendicular/hypotenuse (For some value of k)
= perpendicular/hypotenuse (For some value of k)
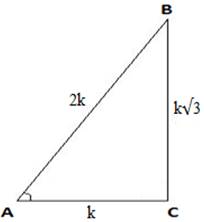
By Pythagoras theorem, (hypotenuse)2 = (perpendicular)2 + (base)2
∴AB2 = BC2 + AC2
(2k)2 = (k√3)2 + AC2
4k2 = 3k2 + AC2
AC2 = (4 - 3)k2
AC2 = k2
→ AC = k, for some number k
Hence, the trigonometric ratios for the given θ are:
sinθ = ![]()
cosθ = AC/AB = k/(2k) = 1/2
tanθ = BC/AC = sinθ /cosθ = (k√3)/k = √k
cotθ = 1/tanθ = AC/BC = k/(k√3) = 1/√3
cosecθ = 1/sinθ = AB/BC = (2k)/(k√3) = 2/√3
secθ = 1/cosθ = AB/AC = (2k)/k = 2
1