We have, tanA = k/(k√3) = BC/AB

Δ ABC is a right angled triangle

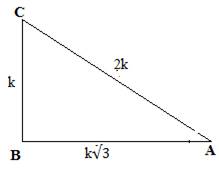
By Pythagoras theorem, (hypotenuse)² = (perpendicular)² + (base)²

∴AC² = BC² + AB²

= AC² = (k)² + (k√3)²

= AC² = k² + 3k²

= AC² = 4k²

→ AC = 2k

∴ sinA = BC/AC = k/(2k) = 1/2

cosA = AB/AC = (k√3)/(2k) = √3/2

sinC = AB/AC = (k√3)/(2k) = √3/2

cosC = = BC/AC = k/(2k) = 1/2

i. sinA cosC + cosA sinC = (1/2)(1/2) + ( √3/2)( √3/2)

=

= 4/4

= 1

∴ RHS = LHS

HENCE PROVED

ii. cosA cosC - sinA sinC = (1/2)(√3/2) - (1/2)(√3/2)

= (√3/4) - (√3/4)

= 0

∴ RHS = LHS

HENCE PROVED