If A and B are acute angles such that tan 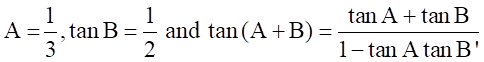, show that A + B = 45°.

Question

Philoid · Accepted Answer

Given: tan (A +B) = and tan A = 1/3, tan B = 1/2

∴ tan(A +B) = = = = 1

∴ tan(A + B) = 1

Also, A and B are acute angles, therefore both A and B are less than 90°. So A + B must be less than 180°.

Therefore, the only possible case for which tan (A+B) = 1 will be when (A + B) equals 45°.

Thus, A + B = 45°