Find the length of tangent drawn to a circle with radius 8 cm from a point 17 cm away from the center of the circle.
Let us consider a circle with center O and radius 8 cm.
The diagram is given as:
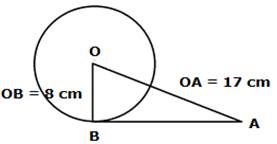
Consider a point A 17 cm away from the center such that OA = 17 cm
A tangent is drawn at point A on the circle from point B such that OB = radius = 8 cm
To Find: Length of tangent AB = ?
As seen OB ⏊ AB
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∴ In right - angled ΔAOB, By Pythagoras Theorem
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
(OA)2 = (OB)2 + (AB)2
(17)2 = (8)2 + (AB)2
289 = 64 + (AB)2
(AB)2 = 225
AB = 15 cm
∴ The length of the tangent is 15 cm.
1