Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
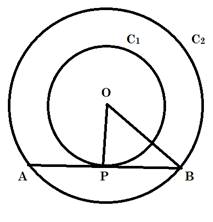
Given: Two concentric circles (say C1 and C2) with common center as O and radius r1 = 6.5 cm and r2 = 2.5 cm respectively.
To Find: Length of the chord of the larger circle which touches the circle C2. i.e. Length of AB.
As AB is tangent to circle C2 and we know that "Tangent at any point on the circle is perpendicular to the radius through point of contact"
So, we have,
OP ⏊ AB
∴ OPB is a right - angled triangle at P,
By Pythagoras Theorem in △OPB
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
We have,
(OP)2 + (PB)2 = (OB)2
r22 + (PB)2 = r12
(2.5)2 + (PB)2= (6.5)2
6.25 + (PB)2 = 42.25
(PB)2 = 36
PB = 6 cm
Now, AP = PB ,
[ as perpendicular from center to chord bisects the chord and OP ⏊ AB ]
So,
AB = AP + PB = PB + PB
= 2PB = 2(6)
= 12 cm