RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 12. Circles

Subject: Maths - Class 10th

Q. No. 7 of Exercise 12A

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

7

From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14 cm, find the perimeter of △PCD.

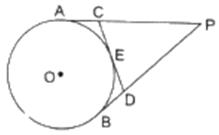
Given : From an external point P, two tangents, PA and PB are drawn to a circle with center O. At a point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. And PA = 14 cm


To Find : Perimeter of △PCD


As we know that, Tangents drawn from an external point to a circle are equal.


So we have


AC = CE …[1] [Tangents from point C]


ED = DB …[2] [Tangents from point D]


Now Perimeter of Triangle PCD


= PC + CD + DP


= PC + CE + ED + DP


= PC + AC + DB + DP [From 1 and 2]


= PA + PB


Now,


PA = PB = 14 cm as tangents drawn from an external point to a circle are equal


So we have


Perimeter = PA + PB = 14 + 14 = 28 cm


Chapter Exercises

Exercise 12A
Exercise 12B
Multiple Choice Questions (MCQ)
Formative Assessment (Unit Test)

More Exercise Questions

1

Find the length of tangent drawn to a circle with radius 8 cm from a point 17 cm away from the center of the circle.
2

A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
3

Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
4

In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
5

In the given figure, PA and PB are the tangent segments to a circle with center 0. Show that the points A, O, B and P are concyclic.
6

In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
7

From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14 cm, find the perimeter of △PCD.
8

A circle is inscribed in a LABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR = 7 cm and CR = 5 cm, find the length of BC.
9

In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6 cm, BC = 7 cm and CD = 4 cm. Find AD.
10

In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
11

In the given figure, O is the center of two concentric circles of radii 4 cm and 6 cm respectively. PA and PB are tangents to the outer and inner circle respectively. If PA = 10 cm, find the length of PB up to one place of decimal.
12

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 6 cm and 9 cm respectively. If the area of ABC = 54 cm2 then find the lengths of sides AB and AC.
13

PQ is a chord of length 4.8 cm of a circle of radius 3 cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
14

Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its center.
15

In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29 cm, AD = 23 cm, LB = 90° and DS = 5 cm then find the radius of the circle.
16

In the given figure, O is the center of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30°, prove that BA : AT = 2 : 1.

Students Store