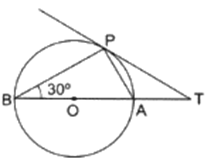
In Given Figure, we have a circle with center O let the radius of circle be r.

Construction : Join OP

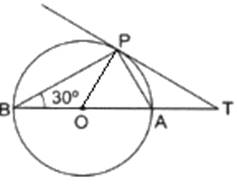
Now, In △APB

∠ABP = 30°

∠APB = 90°

[Angle in a semicircle is a right angle]

By angle sum Property of triangle,

∠ABP + ∠APB + ∠PAB = 180

30° + 90° + ∠PAB = 180

∠PAB = 60°

OP = OA = r [radii]

∠PAB = ∠OPA = 60°

[Angles opposite to equal sides are equal]

By angle sum Property of triangle

∠OPA + ∠OAP + ∠AOP = 180°

60° + ∠PAB + ∠AOP = 180

60 + 60 + ∠AOP = 180

∠AOP = 60°

As all angles of △OPA equals to 60°, △OPA is an equilateral triangle

So, we have, OP = OA = PA = r [1]

∠OPT = 90°

[Tangent at any point on the circle is perpendicular to the radius through point of contact]

∠OPA + ∠APT = 90

60 + ∠APT = 90

∠APT = 30°

Also,

∠PAB + ∠PAT = 180° [Linear pair]

60° + ∠PAT = 180°

∠PAT = 120°

In △APT

∠APT + ∠PAT + ∠PTA = 180°

30° + 120° + ∠PTA = 180°

∠PTA = 30°

So,

We have

∠APT = ∠PTA = 30°

AT = PA

[Sides opposite to equal angles are equal]

AT = r [From 1] [2]

Now,

AB = OA + OB = r + r = 2r [3]

From [2] and [3]

AB : AT = 2r : r = 2 : 1

Hence Proved !