In the given figure, PA and PB are two tangents to the circle with center O. If ∠APB = 50° then what is the measure of ∠OAB.
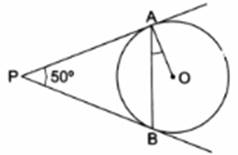
In the given figure, PA and PB are two tangents from common point P
∴ PA = PB
[Tangents drawn from an external point are equal]
∠PBA = ∠PAB
[Angles opposite to equal angles are equal] [1]
By angle sum property of triangle in △APB
∠APB + ∠PBA + ∠PAB = 180°
50° + ∠PAB + ∠PAB = 180° [From 1]
2∠PAB = 130°
∠PAB = 65° [2]
Now,
∠OAP = 90°
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∠OAB + ∠PAB = 90°
∠OAB + 65° = 90° [From 2]
∠OAB = 25°
2