In the given figure, O is the center of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70°, find ∠TRQ.

Question

In the given figure, O is the center of a circle. PT and PQ are tangents to the circle from an external point P. If ∠ TPQ = 70°, find ∠ TRQ.

Philoid · Accepted Answer

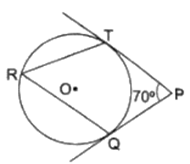
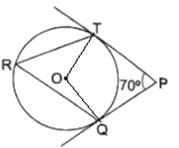
Given: In the figure, PT and PQ are two tangents and ∠TPQ = 70°

To Find: ∠TRQ

Construction: Join OT and OQ

In quadrilateral OTPQ

∠OTP = 90°

[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

∠OQP = 90°

[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

∠TPQ = 70° [Common]

By Angle sum of Quadrilaterals,

In quadrilateral OTPQ we have

∠OTP + ∠OQP + ∠TPQ + ∠TOQ = 360°

90° + 90° + 70° + ∠TOQ = 360°

250° + ∠TOQ = 360

∠TQO = 110°

Now,

As we Know the angle subtended by an arc at the center is double the angle subtended by it at any

point on the remaining part of the circle.

∴ we have

∠TOQ = 2∠TRQ

110° = 2 ∠TRQ

∠TRQ = 55°