In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4 cm and 3 cm respectively. If the area of ΔABC = 21 cm² then find the lengths of sides AB and AC.

Question

Philoid · Accepted Answer

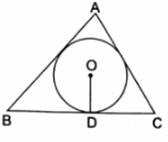
Given: △ABC that is drawn to circumscribe a circle with radius r = 2 cm and BD = 4 cm DC = 3cm

Also, area(△ABC) = 21 cm²

To Find: AB and AC

Now,

As we know tangents drawn from an external point to a circle are equal.

Then,

FB = BD = 4 cm [Tangents from same external point B]

DC = EC = 3 cm [Tangents from same external point C]

AF = EA = x (let) [Tangents from same external point A]

Using the above data, we get

AB = AF + FB = x + 4 cm

AC = AE + EC = x + 3 cm

BC = BD + DC = 4 + 3 = 7 cm

Now we have heron's formula for area of triangles if its three sides a, b and c are given

Where,

So, for △ABC

a = AB = x + 4

b = AC = x + 3

c = BC = 7 cm

⇒

And

Squaring both sides,

21(21) = 12x(x + 7)

12x² + 84x - 441 = 0

4x² + 28x - 147 = 0

As we know roots of a quadratic equation in the form ax² + bx + c = 0 are,

So roots of this equation are,

but x = - 10.5 is not possible as length can't be negative.

So

AB = x + 4 = 3.5 + 4 = 7.5 cm

AC = x + 3 = 3.5 + 3 = 6.5 cm

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4 cm and 3 cm respectively. If the area of ΔABC = 21 cm2 then find the lengths of sides AB and AC.

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4 cm and 3 cm respectively. If the area of ΔABC = 21 cm² then find the lengths of sides AB and AC.