RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 12. Circles

Subject: Maths - Class 10th

Q. No. 9 of Exercise 12B

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

9

In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with center 0. If ∠PRQ = 120°, then prove that OR = PR + RQ.

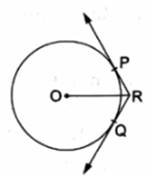
Given : In the figure ,



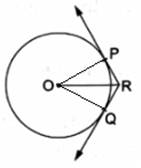
Two tangents RQ and RP are drawn from an external point R to the circle with center O and ∠PRQ = 120°


To Prove: OR = PR + RQ


Construction: Join OP and OQ


Proof :


In △△OPR and △OQR


OP = OQ [radii of same circle]


OR = OR [Common]


PR = PQ …[1]


[Tangents drawn from an external point are equal]


△OPR ≅ △OQR


[By Side - Side - Side Criterion]


∠ORP = ∠ORQ


[Corresponding parts of congruent triangles are congruent]


Also,


∠PRQ = 120°


∠ORP + ∠ORQ = 120°


∠ORP + ∠ORP = 120°


2∠ORP = 120°


∠ORP = 60°


Also, OP ⏊ PR


[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]


So, In right angled triangle OPR,




∴ OR = 2PR


OR = PR + PR


OR = PR + RQ [From 1]


Hence Proved.


Chapter Exercises

Exercise 12A
Exercise 12B
Multiple Choice Questions (MCQ)
Formative Assessment (Unit Test)

More Exercise Questions

1

In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.
2

In the given figure, PA and PB are two tangents to the circle with center O. If ∠APB = 50° then what is the measure of ∠OAB.
3

In the given figure, O is the center of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70°, find ∠TRQ.
4

In the given figure, common tangents AB and CD to the two circles with centers O1 and O2 intersect at E. Prove that AB = CD.
5

If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
6

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4 cm and 3 cm respectively. If the area of ΔABC = 21 cm2 then find the lengths of sides AB and AC.
7

Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle (in cm) which touches the smaller circle.
8

Prove that the perpendicular at the point of contact of the tangent to a circle passes through the center.
9

In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with center 0. If ∠PRQ = 120°, then prove that OR = PR + RQ.
10

In the given figure, a circle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14 cm, BC = 8 cm and CA = 12 cm. Find the lengths AD, BE and CF.
11

In the given figure, 0 is the center of the circle. PA and PB are tangents. Show that AOBP is a cyclic quadrilateral.
12

In two concentric circles, a chord of length 8 cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5 cm then find the radius of the smaller circle.
13

In the given figure, PQ is a chord of a circle with center 0 and PT is a tangent. If ∠QPT = 60°, find ∠P
14

In the given figure, PA and PB are two tangents to the circle with center O. If ∠APB = 60° then find the measure of ∠OAB.

Students Store