In two concentric circles, a chord of length 8 cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5 cm then find the radius of the smaller circle.
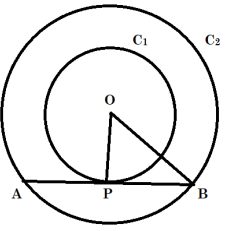
Let us consider circles C1 and C2 with common center as O. Let AB be a tangent to circle C1 at point P and chord in circle C2. Join OB
In △OPB
OP ⏊ AB
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∴ OPB is a right - angled triangle at P,
By Pythagoras Theorem,
[i.e. (Hypotenuse)2 = (Base)2 + (Perpendicular)2]
(OB)2 = (OP)2 + (PB)2
Now, 2PB = AB
[As we have proved above that OP ⏊ AB and Perpendicular drawn from center to a chord bisects the chord]
2PB = 8 cm
PB = 4 cm
(OB)2 = (5)2 + (4)2
[As OP = 5 cm, radius of inner circle]
(OB)2 = 41
⇒ OB = √41 cm