RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 12. Circles

Subject: Maths - Class 10th

Q. No. 13 of Exercise 12B

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

13

In the given figure, PQ is a chord of a circle with center 0 and PT is a tangent. If ∠QPT = 60°, find ∠P

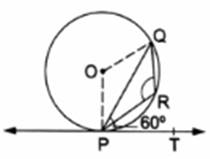
Given : , PQ is a chord of a circle with center 0 and PT is a tangent and ∠QPT = 60°.


To Find : ∠PRQ


∠OPT = 90°


∠OPQ + ∠QPT = 90°


∠OPQ + 60° = 90°


∠OPQ = 30° … [1]


Also.


OP = OQ [radii of same circle]


∠OQP = ∠OPQ [Angles opposite to equal sides are equal]


From [1], ∠OQP = ∠OQP = 30°


In △OPQ , By angle sum property


∠OQP + ∠OPQ + ∠POQ = 180°


30° + 30° + ∠POQ = 180°


∠POQ = 120°


As we know, the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.


So, we have


2∠PRQ = reflex ∠POQ


2∠PRQ = 360° - ∠POQ


2∠PRQ = 360° - 120° = 240°


∠PRQ = 120°


Chapter Exercises

Exercise 12A
Exercise 12B
Multiple Choice Questions (MCQ)
Formative Assessment (Unit Test)

More Exercise Questions

1

In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.
2

In the given figure, PA and PB are two tangents to the circle with center O. If ∠APB = 50° then what is the measure of ∠OAB.
3

In the given figure, O is the center of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70°, find ∠TRQ.
4

In the given figure, common tangents AB and CD to the two circles with centers O1 and O2 intersect at E. Prove that AB = CD.
5

If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
6

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4 cm and 3 cm respectively. If the area of ΔABC = 21 cm2 then find the lengths of sides AB and AC.
7

Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle (in cm) which touches the smaller circle.
8

Prove that the perpendicular at the point of contact of the tangent to a circle passes through the center.
9

In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with center 0. If ∠PRQ = 120°, then prove that OR = PR + RQ.
10

In the given figure, a circle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14 cm, BC = 8 cm and CA = 12 cm. Find the lengths AD, BE and CF.
11

In the given figure, 0 is the center of the circle. PA and PB are tangents. Show that AOBP is a cyclic quadrilateral.
12

In two concentric circles, a chord of length 8 cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5 cm then find the radius of the smaller circle.
13

In the given figure, PQ is a chord of a circle with center 0 and PT is a tangent. If ∠QPT = 60°, find ∠P
14

In the given figure, PA and PB are two tangents to the circle with center O. If ∠APB = 60° then find the measure of ∠OAB.

Students Store