In the given figure, point P is 26 cm away from the center 0 of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then, the radius of the circle is
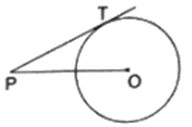
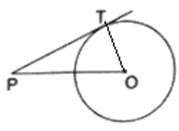
We have given, PT is a tangent drawn at point T on the circle and OP = 26 cm and PT = 24 cm
Join OT
∴ OT ⏊ TP
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
So, In △OTP we have,
By Pythagoras Theorem,
[i.e. (Hypotenuse)2 = (Base)2 + (Perpendicular)2]
(OP)2 = (OT)2 + (PT)2
(26)2 = (OT)2 + (24)2
(OT)2 = 676 - 576
(OT)2 = 100
OT = 10 cm
Hence, radius of circle is 10 cm.
7