In the given figure, O is the center of two concentric circles of radii 6 cm and 10 cm. AB is a chord of outer circle which touches the inner circle. The length of chord AB is
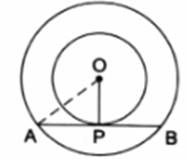
Given: Two concentric circles (say C1 and C2) with common center as O and radius r1 = 6 cm(inner circle) and r2 = 10 cm (outer circle) respectively.
To Find : Length of the chord AB.
As AB is tangent to circle C1 and we know that "Tangent at any point on the circle is perpendicular to the radius through point of contact"
So, we have,
OP ⏊ AB
∴ OPB is a right - angled triangle at P,
By Pythagoras Theorem in △OPB
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
We have,
(OP)2 + (PA)2 = (OA)2
r12 + (PA)2 = r22
(6)2 + (PA)2= (10)2
36 + (PA)2 = 100
(PA)2 = 64
PA = 8 cm
Now, PA = PB ,
[ as perpendicular from center to chord bisects the chord and OP ⏊ AB]
So,
AB = PA + PB = PA + PA = 2PA = 2(8) = 16 cm