In the given figure, O is the center of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ = 70°, then ∠TPQ is equal to

Question

In the given figure, O is the center of a circle, PQ is a chord and PT is the tangent at P. If ∠ POQ = 70°, then ∠ TPQ is equal to

Philoid · Accepted Answer

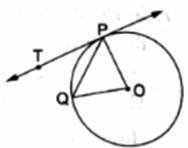
In △OPQ

∠POQ = 70° [Given]

OP = OQ [radii of same circle]

∠OQP = ∠OPQ [Angles opposite to equal sides are equal]

By angle sum Property of triangle,

∠POQ + ∠OQP + ∠OPQ = 180°

70° + ∠OPQ + ∠OPQ = 180°

2 ∠OPQ = 110°

∠OPQ = 55°

Now,

∠OPT = 90°

[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

∠OPQ + ∠TPQ = 90°

55° + ∠TPQ = 90°

∠TPQ = 35°