If PA and PB are two tangents to a circle with center O such that ∠AOB = 110° then ∠APB is equal to

Question

If PA and PB are two tangents to a circle with center O such that ∠ AOB = 110° then ∠ APB is equal to

Philoid · Accepted Answer

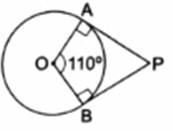
As AP and BP are tangents to given circle,

We have,

OA ⏊ AP and OB ⏊ BP

[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

So, ∠OAP = ∠OBP = 90°

In quadrilateral AOBP,

By angle sum property of quadrilateral, we have

∠OAP + ∠OBP + ∠AOB + ∠APB = 360°

90° + 90° + 110° + ∠APB = 360°

∠APB = 70°