RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 12. Circles

Subject: Maths - Class 10th

Q. No. 21 of Multiple Choice Questions (MCQ)

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

21

If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm then the length of each tangent is


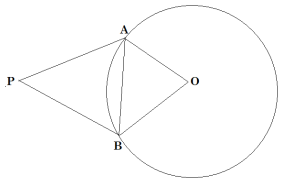
Let us consider a circle with center O and AP and BP are two tangents such that angle of inclination i.e. ∠APB = 60°


Joined OA, OB and OP.


To Find : Length of tangents


Now,


PA = PB [Tangents drawn from an external point are equal] [1]


In △AOP and △BOP


PA = PB [By 1]


OP = OP [Common]


OA = OB [radii of same circle]


△AOP ≅△BOP


[By Side - Side - Side Criterion]


∠OPA = ∠OPB


[Corresponding parts of congruent triangles are congruent]


Now,


∠APB = 60° [Given]


∠OPA + ∠OPB = 60°


∠OPA + ∠OPA = 60°


2 ∠OPA = 60°


∠OPA = 30°


In △AOP


OA ⏊ PA


[Tangents drawn at a point on circle is perpendicular to the radius through point of contact


∴ AOP is a right - angled triangle.


So, we have





⟹PA = 3√3 cm


From [1]


PA = PB = 4 cm


i.e. length of each tangent is 3√3 cm

Chapter Exercises

Exercise 12A
Exercise 12B
Multiple Choice Questions (MCQ)
Formative Assessment (Unit Test)

More Exercise Questions

1

The number of tangents that can be drawn from an external point to a circle is
2

In the given figure, RQ is a tangent to the circle with center O. If SQ = 6 cm and QR = 4 cm, then OR is equal to
3

In a circle of radius 7 cm, tangent PT is drawn from a point P such that PT = 24 cm. If O is the center of the circle, then length OP = ?
4

Which of the following pairs of lines in a circle cannot be parallel?
5

The chord of a circle of radius 10 cm subtends a right angle at its center. The length of the chord (in cm) is
6

In the given figure, PT is a tangent to the circle with center O. If OT = 6 cm and OP = 10 cm, then the length of tangent PT is
7

In the given figure, point P is 26 cm away from the center 0 of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then, the radius of the circle is
8

PQ is a tangent to a circle with center O at the point P. If ΔOPQ is an isosceles triangle, then ∠OQP is equal to
9

In the given figure, AB and AC are tangents to the circle with center O such that ∠BAC = 40°. Then, ∠BOC is equal to
10

If a chord AB subtends an angle of 60° at the center of a circle, then the angle between the tangents to the circle drawn from A and B is
11

In the given figure, O is the center of two concentric circles of radii 6 cm and 10 cm. AB is a chord of outer circle which touches the inner circle. The length of chord AB is
12

In the given figure, AB and AC are tangents to a circle with center 0 and radius 8 cm. If OA = 17 cm, then the length of AC (in cm) is
13

In the given figure, 0 is the center of a circle, AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at the point A then ∠BAT = ?
14

In the given figure, O is the center of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ = 70°, then ∠TPQ is equal to
15

In the given figure, AT is a tangent to the circle with center O such that OT = 4 cm and ∠OTA = 30°. Then, AT = ?
16

If PA and PB are two tangents to a circle with center O such that ∠AOB = 110° then ∠APB is equal to
17

In the given figure, the length of BC is
18

In the given figure, if ∠AOD = 135° then ∠BOC is equal to
19

In the given figure, 0 is the center of a circle and PT is the tangent to the circle. If PQ is a chord such that ∠QPT = 50° then ∠POQ = ?
20

In the given figure, PA and PB are two tangents to the circle with center O. If ∠APB = 60° then ∠OAB is
21

If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm then the length of each tangent is
22

In the given figure, PQ and PR are tangents to a circle with center A. If ∠QPA = 27° then ∠QAR equals
23

In the given figure, PA and PB are two tangents drawn from an external point P to a circle with center C and radius 4 cm. If PA ⏊ PB, then the length of each tangent is
24

If PA and PB are two tangents to a circle with center O such that ∠APB = 80°. Then, ∠AOP = ?
25

In the given figure, O is the center of the circle. AB is the tangent to the circle at the point P. If ∠APQ = 58° then the measure of ∠PQB is
26

In the given figure, O is the center of the circle. AB is the tangent to the circle at the point P. If ∠PAO = 30° then ∠CPB + ∠ACP is equal to
27

In the given figure, PQ is a tangent to a circle with center O. A is the point of contact. If ∠PAB = 67°, then the measure of ∠AQB is
28

In the given figure, two circles touch each other at C and AB is a tangent to both the circles. The measure of ∠ACB is
29

O is the center of a circle of radius 5 cm. At a distance of 13 cm from O, a point P is taken. From this point, two tangents PQ and PR are drawn to P the circle. Then, the area of quad. PQOR is
30

In the given figure, PQR is a tangent to the circle at Q, whose center is O and AB is a chord parallel to PR such that ∠BQR = 70°. Then, ∠AQB =?
31

The length of the tangent from an external point P to a circle of radius 5 cm is 10 cm. The distance of the point from the center of the circle is
32

In the given figure, 0 is the center of a circle, BOA is its diameter and the tangent at the point P meets BA extended at T. If ∠PBO = 30° then ∠PTA = ?
33

In the given figure, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm then the perimeter of ΔEDF is
34

To draw a pair of tangents to a circle, which is inclined to each other at an angle of 45°, we have to draw tangents at the end points of those two radii, the angle between which is
35

In the given figure, O is the center of a circle; PQL and PRM are the tangents at the points Q and R respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then, ∠QSR = ?
36

In the given figure, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2 then the length of side PQ is
37

In the given figure, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm then the length of QR is
38

In the given figure, quad. ABCD is circumscribed, touching the circle at P, Q, R and S. If AP = 5 cm, BC = 7 cm and CS = 3 cm. Then, the length AB = ?
39

In the given figure, quad. ABCD is circumscribed, touching the circle at P, Q, R and S. If AP = 6 cm, BP = 5 cm, CQ = 3 cm and DR = 4 cm then perimeter of quad. ABCD is
40

In the given figure, O is the center of a circle, AB is a chord and AT is the tangent at A. If ∠AOB = 100° then ∠BAT is equal to
41

In a right triangle ABC, right - angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle is
42

In the given figure, a circle is inscribed in a quadrilateral ABCD touching its sides AB, BC, CD and AD at P, Q, R and S respectively. lithe radius of the circle is 10 cm, BC = 38 cm, PB = 27 cm and AD⏊ CD then the length of CD is
43

In the given figure, LABC is right - angled at B such that BC = 6 cm and AB = 8 cm. A circle with center O has been inscribed inside the triangle. OP ⊥AB, OQ ⊥BC and OR ⊥AC. If OP = OQ = OR = x cm then x = ?
44

Quadrilateral ABCD is circumscribed to a circle. If AB = 6 cm, BC = 7 cm and CD = 4 cm then the length of AD is
45

In the given figure, PA and PB are tangents to the given circle such that PA = 5 cm and ∠APB = 60°. The length of chord AB is
46

In the given figure, DE and DF are tangents from an external point D to a circle with center A. If DE = 5 cm and DE ⊥ DF then the radius of the circle is
47

In the given figure, three circles with centers A, B, C respectively touch each other externally.

If AB = 5 cm, BC = 7 cm and CA = 6 cm then the radius of the circle with center A is
48

In the given figure, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm then the length of AP is
49

In the given figure, O is the center of two concentric circles of radii 5 cm and 3 cm. From an external point P tangents PA and PB are drawn to these circles. If PA = 12 cm then PB is equal to
50

Which of the following statements is not true?
51

Which of the following statements is not true?
52

Which of the following statements is not true?
53

Assertion - and - Reason Type

Each question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer, use the following code:
54

Assertion - and - Reason Type

Each question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer, use the following code
55

Assertion - and - Reason Type

Each question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer, use the following code:

Students Store