In the given figure, PQ is a tangent to a circle with center O. A is the point of contact. If ∠PAB = 67°, then the measure of ∠AQB is

Question

In the given figure, PQ is a tangent to a circle with center O. A is the point of contact. If ∠ PAB = 67°, then the measure of ∠ AQB is

Philoid · Accepted Answer

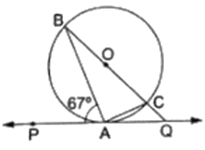
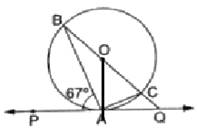
In the given Figure, Join OA

Now,

OA ⏊ PQ

[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

∠OAP = ∠OAQ = 90° [1]

∠OAB + ∠PAB = 90°

∠OAB + 67° = 90°

∠OAB = 23°

Now,

∠BAC = 90°

[Angle in a semicircle is a right angle]

∠OAB + ∠OAC = 90°

23° + ∠OAC = 90°

∠OAC = 67°

∠OAQ = 90° [From 1]

∠OAC + ∠CAQ = 90°

67° + ∠CAQ = 90°

∠CAQ = 23° [2]

Now,

OA = OC

[radii of same circle]

∠OCA = ∠OAC

[Angles opposite to equal sides are equal]

∠OCA = 67°

∠OCA + ∠ACQ = 180° [Linear Pair]

67° + ∠ACQ = 180°

∠ACQ = 113° [3]

Now, In △ACQ By Angle Sum Property of triangle

∠ACQ + ∠CAQ + ∠AQC = 180°

113° + 23° + ∠AQC = 180° [By 2 and 3]

∠AQC = 44°