In the given figure, PQR is a tangent to the circle at Q, whose center is O and AB is a chord parallel to PR such that ∠BQR = 70°. Then, ∠AQB =?

Question

In the given figure, PQR is a tangent to the circle at Q, whose center is O and AB is a chord parallel to PR such that ∠ BQR = 70°. Then, ∠ AQB =?

Philoid · Accepted Answer

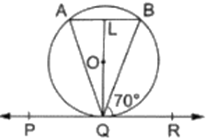
In given figure, as PR is a tangent

OQ ⏊ PR

[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

⟹LQ ⏊ PR

⟹LQ ⏊ AB

[As, AB || PR]

AL = LB

[Perpendicular from center to the chord bisects the chord]

Now,

∠LQR = 90°

∠LQB + ∠BQR = 90°

∠LQB + 70° = 90°

∠LQB = 20°…[1]

In △AQL and △BQL

∠ALQ = ∠BLQ [Both 90° as LQ ⏊ AB]

AL = LB [Proved above]

QL = QL [Common]

△AQL ≅ △BQL

[Side - Angle - Side Criterion]

∠LQA = ∠LQB

[Corresponding parts of congruent triangles are congruent]

∠AQB = ∠LQA + ∠LQB = ∠LQB + ∠LQB

= 2∠LQB = 2(20) = 40° [By 1]