The length of the tangent from an external point P to a circle of radius 5 cm is 10 cm. The distance of the point from the center of the circle is
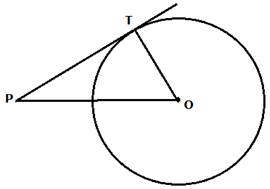
Let us consider a circle with center O and TP be a tangent at point A on the circle, Joined OT and OP
Given Length of tangent, TP = 10 cm, and OT = 5 cm [radius]
To Find : Distance of center O from P i.e. OP
Now,
OP ⏊ TP
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
So OPT is a right - angled triangle,
By Pythagoras Theorem in ΔOPB
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
(OT)2 + (TP)2 = (OP)2
(OP)2 = (5)2 + (10)2
(OP)2 = 25 + 100 = 125
OP = √125 cm
31